
SELF
ASSEMBLING OF THE DHS
The simulations of the DHS, at low densities and temperatures, show a strong tendency to form clusters of different topologies: rings, chains and several types of branched clusters.
In order to obtain a
quantitative caracterization of this strucuture (the number of clusters of each
type present in one simulation) we start by defining a cut-off distance Rc
(a little bit larger than the diameter of the spheres), so that if two particles
are placed at a distance less than Rc , they belong to the same cluster. In order to
classify the clusters
thus obtained, we start by classifying each particle as follows:
(0)
free particle: particle with no other particle at a distance less than Rc
.
(1)
end particle: particle with only one other particle at a distance less than Rc
.
(2)
interior particle: particle with two and only two particles at a distance
less than Rc .
(3)
defect particle: particle with more than two other particles at a distance
less than Rc .
Then, a definition of
cluster types is possible:
Rings: clusters with only interior particles.
Chains: clusters with two (and only two) end particles.
Defect clusters: all clusters with at least one defect particle.
In the next figure we represent the final result of this classification
for a specific configuration of a 2-dimensional DHS:

From
the configurations that were kept it is possible
to calculate several properties of rings, chains and defect clusters. In
the following we describe the results obtained for a 2 - dimensional DHS with 5776
particles.
We
have calculated the radius of gyration and the energy per particle. The
radius of gyration is a measure of the mean distance of the particles in a
cluster to its center of mass. We
found that, for both chains, rings and defect clusters, it is a power of the
number of particles. The measured exponent is close to 0.75, meaning that the
clusters are fractals (the fractal dimension is just 1/0.75)
with conformational properties similar to
2-dimensional self avoiding random walks.
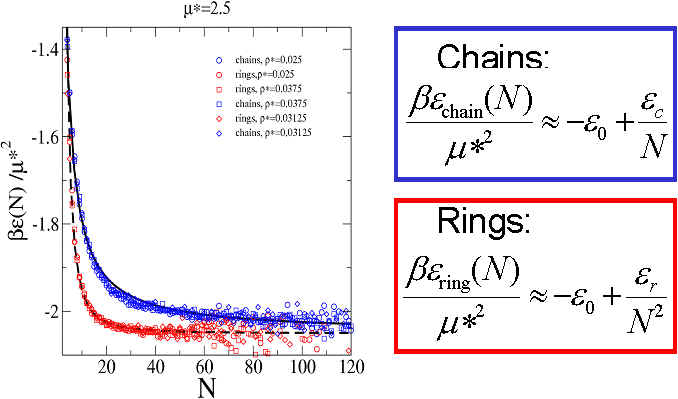
The energy per particle of chains and rings is, to a good
approximation, the sum of a
constant (e0
m*2,
that is found to be the same for chains and rings) and a correction for
short clusters that depends on 1/N for chains and on 1/N2 for rings.
The next figure shows a comparison between the simulation results this form for
the energy
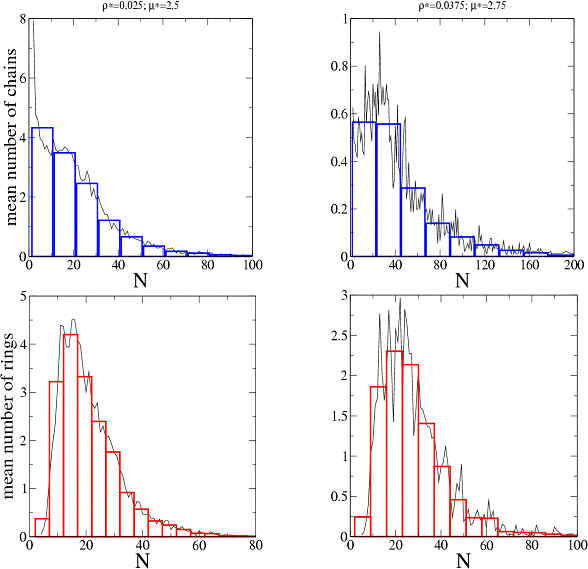
We have calculated also the length distributions for the three types of clusters, i.e., the mean number of clusters of each size and of each type present in each simulation. These results for two simulations and for chains (blue) and rings (red) are shown in the next figure. The ring’s distributions exhibit a maximum and decay faster than those of chains. The system is thus polydisperse with well defined length (or mass) distributions that depend on the total density and the interactions.
By following individual clusters during a simulation we conclude that, although their length and size distributions fluctuate around well defined values, the clusters form, break and recombine in several ways. That is, the equilibrium state is not described by “static” clusters (i.e. formed by the same particles) but by clusters that keep exchanging particles among them. Other calculations show that the contribution of the interaction between clusters to the internal energy of the system is less than 1%.
These results suggest a simple hypothesis for the structure of the DHS at low densities and temperatures: the DHS is an IDEAL SELF ASSEMBLING SYSTEM, i.e., a system that exhibits spontaneous aggregation in non interacting clusters at chemical equilibrium.
It is possible to show that, within this framework, the distribution of clusters of type k must be proportional to the partition function of the clusters. This distribution is written as,

where
r*k(N)
is
the number of clusters (of type k formed by N particles) per unit volume,
q
k(N) is the corresponding partition function
and m is
the chemical potential.
The fact that the chains and rings are conformationally similar to self avoiding random walks and their internal energy is known, allows us to write the partition functions as,
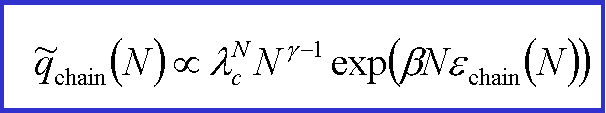
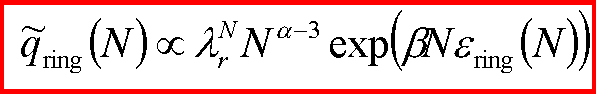
In
these expressions a
and g
are universal exponents of polymer theory. Combining the
above equations it is possible to define universal distributions
of the number of chains and rings (in the sense that they depend only on a
and g
). In
the next figure we show the comparison between the distributions
calculated from simulations and the universal theoretical prediction obtained
for d=2 (with, a
= 0.5 and g
=1.33).
We represent data from 6 different simulations. Nc is the mean
chain length.
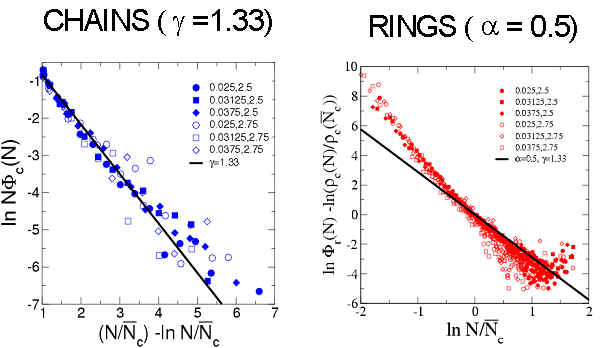
The good agreement between the simulation data and the theoretical prediction shows that at the densities and dipole moments studied in our work, the complex structure of the DHS can be described as the self-assembly of ideal clusters. Under these conditions the DHS is analogous to equilibrium polymers, simpler systems where monomers aggregate into chains and rings at chemical equilibrium.
The major open question, that is currently under study, concerns the existence and nature of a phase transition, that is supposed to occur at higher densities.