Research Investigação
Monte Carlo Simulations of Deposition of Dipolar Particles
One of the most popular models used to study the growth of deposits is the so-called diffusion limitted deposition (DLD) that is closely related to DLA or diffusion limitted aggregation. In DLD particles are dropped one by one, from a random position at height H, in a box of size L. Each particle moves in a random walk until i) it aggregates irreversibly at the substrate or as the nearest neighbour of a deposited particle or ii) it leaves the box from the top, when it reaches a height H out (see figure).
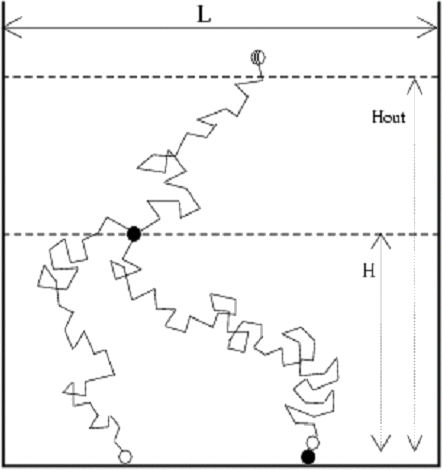
At long times this process yields deposits that consist of several trees that compete to grow. Numerical simulations have shown that the growth of several quantities is characterised by power laws with exponents that are universal [1]. Examples are the density of particles at a given height, the height of the trees, the number of trees of a given size, etc.
Here we consider the deposition of dipolar particles, that is particles that carry a permanent dipole and interact with the deposited particles through this long-ranged anisotropic interaction. The effect of the interactions is controlled by a single parameter, the effective temperature T* or inverse dipole moment. The particles move randomly as in DLD but new positions are accepted according to a Metropolis rule, by comparing the interaction energy of the particle with the deposit before and after each move. At T*=infinity all moves are accepted and the model is identical to DLD. At T*=0 the only acceptable moves are those that lower the energy at each step. In order to speed up the simulations we discretised space and considered the previous model on a square lattice (two dimensional model).
In the next figure we show two typical deposits at high (T*=0.1) and low (T*=0.0001) temperatures. The size is L=800 lattice constants. The colour code illustrates the order in which the particles are aggregated: the first 5000 are black, the next 5000 red, etc.
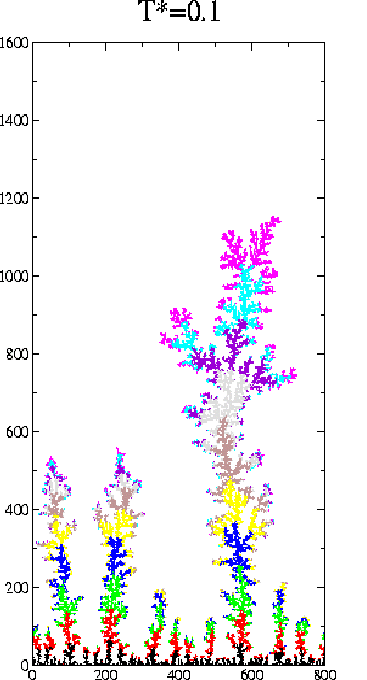
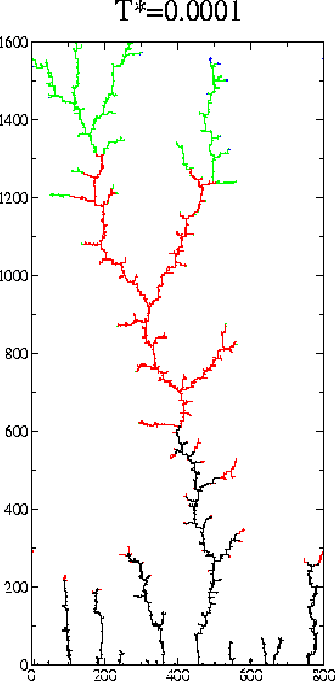
These figures suggest a marked difference between the high and low temperature deposits. At low temperatures the density of the deposits is lower and there are fewer trees. The trees appear to be anisotropic and this anisotropy is temperature dependent.
The major question raised by the previous results is the following: does the universality class of dipolar DLD depend on the temperature?
To address this question we generated about 50 deposits at different temperatures and box sizes and concluded that the dipolar interactions are indeed responsible for an additional non-universal scaling regime, that we called the initial regime. The initial regime is characterised by a power law growth with exponents that do depend on temperature. This regime, however, crosses over to the universal DLD intermediate regime, at sufficiently long times. The crossover time may be extremely long at low temperatures.
The next figure is an example of the calculations that support our conclusions. We have plotted the mean height of the largest tree, H l , as a function of the tree size (or number of particles), s, at a temperatureT*=0.001 (L=200 triangles, L=400 diamonds, L=800 squares and L=1600 circles).
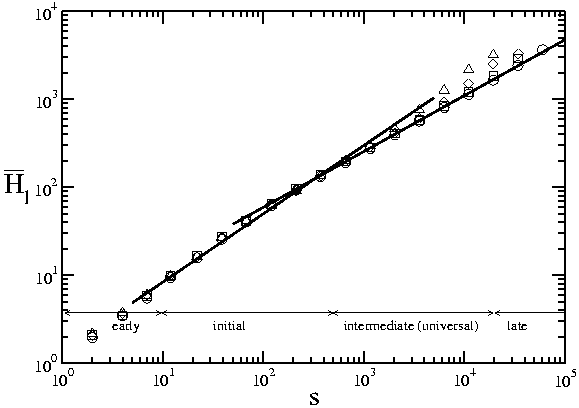
In the previous (log-log) plot we distinguish the two extreme regimes. They correspond to: the early stage regime, for s<10, where the deposit begins to form and the late-stage regime, for very large s, where H l grows linearly with s. Note that the crossover to the late-stage regime occurs at a value of s that increases with the system size L. In DLD there is a universal intermediate regime charaterised by a power law growth of H l with s, with an exponent close to 0.65, for several decades of s, delimited by the early and late-stage regimes.
The last figure illustrates what happens when the dipolar interactions are included. We found two power-law growth regimes rather than the single intermediate DLD regime. We call these the initial and the intermediate scaling regimes. The intermediate scaling regime turns out to be identical to the intermediate DLD regime, and we found that at all temperatures this universal regime obtains for sufficiently large system sizes. By contrast, the initial regime is characterised by power-law growth with exponents that depend on temperature (the slope of the log-log plot depends on the strength of the dipolar interactions). In particular, at T*=0.001 the exponent of H l vs s in the initial regime is close to 0.75, significantly larger than 0.65 the universal DLD exponent. Finally, this non-universal exponent increases as the effective interactions increase.
