Non-linear Dynamics and Waves Group
Nonlinear Dynamics and Waves
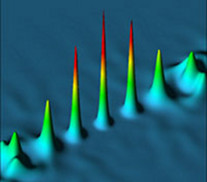
V. Konotop et al. Phys. Rev. A 72 2005
Nonlinear partial differential equations (PDEs) are mathematical models for the time evolution of systems with infinitely many degrees of freedom. The signature of nonlinear behaviour is that 'the whole is more than the sum of its parts' and in nonlinear systems the interactions may lead to the emergence of spatially or temporally coherent structures. Such emergent structures are very much 'things', having their own features, sizes, lifetimes, and peculiar ways of interacting. In this sense, they 'wipe out' the underlying degrees of freedom and may display characteristic collective dynamics.
A soliton is a remarkable example of such a coherent structure. Being a solution of an exactly integrable equation, it preserves its shape and speed not only during temporal evolution but also after collisions with other solitons or linear waves -the particle like property due to which solitary waves were named solitons.
Solitons and Nonlinear Waves
The first observation of a (hydrodynamic) solitary wave was made on a canal in 1834 by a Scottish engineer, John Scott Russell, and the essential features of the problem were put into equation in 1895 by Korteweg and de Vries (KdV) in their shallow water wave theory. The KdV equation was rediscovered much later, in connection with one of the first dynamics simulations carried out on a computer. In 1955, Fermi, Pasta, and Ulam (FPU) simulated a chain of harmonic oscillators coupled with a quadratic nonlinearity and investigated how the energy in one mode spreads throughout the rest. They found that the system cycled periodically, implying that it was 'much more integrable' than they had thought. Zabusky and Kruskal (1965) rederived the KdV equation as the continuum limit of the FPU model, and reported numerical observations of KdV solitons, which they related to the FPU recurrence.
The search for analytic methods to obtain this and other types of exact solutions led to an exponential growth of the field, triggered by the papers of Gardner, Greene, Kruskal and Miura (1967), Zakharov and Shabat (1972), Ablowitz, Kaup, Newell and Segur (1973), that revealed the existence of a large class of nonlinear PDEs that are integrable, on one hand, and of great physical relevance on the other.
Nonlinear waves are relevant in many branches of physics. Soliton bearing equations model surface ocean waves, pressure waves in liquid-gas bubble mixtures, propagation of crystal defects and domain walls in ferromagnetic materials, dynamics of atomic lattices, macromolecules, light propagation along optical waveguides, electromagnetic waves in nonlinear photonic crystals, traffic problems, etc. At present the most exciting (measured by the number of published papers) nonlinear medium is the Bose-Einstein condensate (BEC) predicted by Bose and Einstein almost a century ago and realized experimentally only in 1995. The temperature where this state of matter occurs is ~10-9 K and it is considered the coldest in the Universe.
The properties of conservative nonlinear systems give us a unifying perspective of the different physical contexts, and an understanding of the mechanisms behind the organised collective modes. Soliton solutions discussed above are not the only manifestation of nonlinear waves. Among others we mention resonant mode interactions, shock waves, nonliner periodic waves and soliton trains, modulations instabilities, collapse, etc.
Nonlinear Lattices
Another important class of nonlinear dynamical systems (sometimes also allowing solitonic solutions) are nonlinear lattices. These are systems of (a great number of) coupled ordinary differential equations. They arise naturally in the spatial discretisation of nonlinear partial differential equations, which is required for their numerical integration, and in a variety of physical phenomena including the dynamic description of solids, wave propagation in periodic media, etc. The latter are examples of systems ranging from molecular crystals to interacting biological species that are modeled directly in terms of nonlinear lattices, meaning that we are considering a spatial grid, instead of continuous space coordinates. The development of analytic tools for these systems, and the relation between their properties and those of their continuous conterparts, are a source of interesting problems.
[ Further reading ]
- Solitons and Nonlinear Wave Equations, R. K. Dodd, J. C. Eilbeck, J. D. Gibbon, and H. C. Morris, Academic Press, London, 1982
- Solitons and Inverse Scattering Transform, M. J. Ablowitz and H. Segur, SIAM, Philadelphia, 1981
[ Related sites ]
- Heriot-Watt University's page on solitons.
- Russell's observations: see a modern recreation.
- Press release of the Nobel prizes awarded to the experimental realization of the BEC.
- BEC homepage at Georgia Southern University.
